In this article, we will explore the theory and calculation of the discounted payback period, a key financial metric used in investment analysis. We will walk through its significance, break down the formula, and provide practical examples to illustrate how it is applied in real-world scenarios.
When evaluating investments, businesses and investors often seek to understand how quickly they can recover their initial costs. While the traditional payback period provides a simple way to measure this, it has a major drawback—it ignores the time value of money.
This is where the discounted payback period comes in. By factoring in the present value of future cash flows, the discounted payback period offers a more accurate assessment of when an investment truly breaks even. In this article, we will explore its significance, break down the calculation process, and provide practical examples to illustrate its application in real-world financial analysis.
Table of Contents
However, before delving into the specifics of the discounted payback period, it is essential to first establish a clear understanding of the payback period itself.
If you already know what is Payback period and the process of its calculation, you can skip the part and continue from the topic of discounted payback period.
What is the Payback Period?
The payback period refers to the amount of time required to recover the initial investment made in a project through the project’s cash flows. Essentially, it measures how quickly a business “gets its money back.”
How to calculate payback period?
Payback period formula:
$$ \text{Payback} = \text{Years before full recovery} + \frac{\text{Unrecovered amount}}{\text{Cash flow in recovery year}} $$
Example:
- Initial Investment: $1,000
- Year 1: $500, Cumulative Cash Flow: -$500
- Year 2: $400, Cumulative Cash Flow: -$100
- Year 3: $300, Cumulative Cash Flow: $200Here, full recovery happens between Year 2 and Year 3. The payback is:
$$ 2 + \frac{100}{300} = 2.33 \, \text{years} $$
This calculation shows that it takes 2.33 years to fully recover the initial investment.
This is actually how you calculate the Payback period.
If you want to calculate the payback period for two projects and compare them, you’ll have to choose the project that comes up with the shorter period. But always keep in mind if the projects are independent or mutually exclusive.
In this figure, we have calculated the payback period for two projects using the same payback period calculation method and formula.
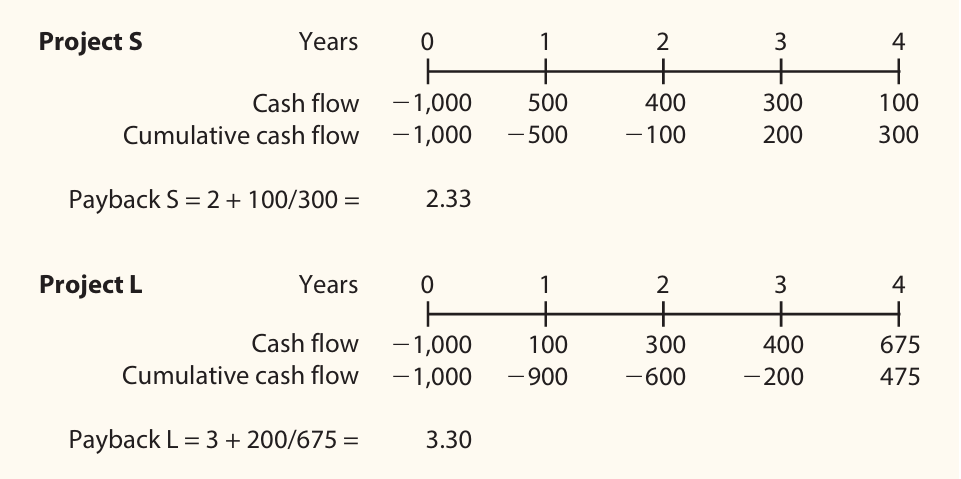
Following the figure you can draw a timeline of a project, put the amount of cashflows year-wise, and cumulative cash flows, and then find out the time using the payback period formula. Drawing a timeline gives you a better representation of the project and helps you calculate more easily.
We can see that, how easy calculating the payback period is and figuring out the number of years we need to recover the initial investment. But the payback period has a major flaw that makes it traditional and most companies avoid calculating the payback period.
Flaws of the Payback Period
Ignores the Time Value of Money: A dollar today is more valuable than a dollar in the future, but this method treats all cash flows equally.
The time value of money means that money you have today can grow over time if invested, making it more valuable than the same amount in the future. However, the payback period method assumes all cash flows are worth the same, ignoring how inflation or investment returns can change their value over time. This can lead to less accurate decisions when comparing projects.
What is the Discounted Payback Period?
Discounted Payback Period is a more advanced way of calculating the payback period of a project. The discounted payback period accounts for the time value of money by discounting the project’s cash flows using the firm’s cost of capital (WACC).
It helps you figure out how long it will take to recover the initial investment after adjusting the fact that future money is worth less than today’s money.
Why is Discounted Payback Period Better than Payback Period?
The discounted payback period solves some of the issues associated with the regular payback period:
- Incorporates the Time Value of Money: By discounting future cash flows, it provides a more accurate view of when the project breaks even.
- More Reliable for Decision-Making: It reflects the true cost of capital and gives a clearer picture of when the investment is recovered.
Discounted Payback Period formula
The discounted Payback period formula is the same as the payback period formula
$$ \text{Payback} = \text{Years before full recovery} + \frac{\text{Unrecovered amount}}{\text{Cash flow in recovery year}} $$
But here, you need to understand another formula to find out the discounted amount of the future cash flows, this is:
$$ \text{Discounted Cash Flow} = \frac{\text{Cash Flow}}{(1 + r)^t} $$
Where:
- r = Discount rate (cost of capital)
- T = Year in which the cash flow occurs
This formula is the same as the formula for calculating the present value of money.
How to calculate the discounted payback period?
Calculating the discounted payback period for the same project is shown in the above figure.

In this figure, you can see that we have calculated the discounted cash flow for each year using the formula discounted cash flow, then we have calculated the cumulative discounted cash flows, and then using the actual discounted Payback period formula we have figured out the time.
Note that, in the question paper you will be provided with the amount of cash flows with a discount rate but if you’re conducting any research, you can estimate the cash flows of a project by reading the blog I’ve written “Estimation of Cash Flows in Capital Budgeting”
Conclusion
The discounted payback period is a valuable financial metric that refines the traditional payback period by incorporating the time value of money. Unlike the regular payback method, it provides a more accurate estimate of when an investment is truly recovered, making it a more reliable tool for decision-making. By discounting future cash flows using the firm’s cost of capital, businesses can assess project viability with greater precision, especially for long-term, high-cost investments.
Understanding how to calculate the discounted payback period ensures better financial planning and risk management. Whether you’re comparing projects or analyzing investment returns, this method helps you make more informed, data-driven decisions. If you have any questions about the discounted payback period formula or calculation, feel free to ask!
FAQs on Discounted Payback Period
1. What is the difference between the payback and discounted payback periods?
The payback period calculates the time required to recover an investment without considering the time value of money. In contrast, the discounted payback period adjusts future cash flows for discounting, providing a more accurate estimate of when an investment is recovered.
2. Why is the discounted payback period important in investment analysis?
The discounted payback period is important because it accounts for the time value of money, ensuring that future cash flows are appropriately discounted. This makes it a more reliable metric for evaluating the feasibility of long-term projects.
3. What are the limitations of the discounted payback period?
While it improves upon the traditional payback period, the discounted payback period still does not account for cash flows beyond the recovery period. This means it does not measure overall project profitability, making it less effective for evaluating long-term returns.
4. What is a good discounted payback period for a project?
There is no universal “good” discounted payback period—it depends on the industry, project type, and investment risk. A shorter payback period is generally preferred, but businesses should also consider profitability, risk, and return on investment.
5. How does the discount rate affect the discounted payback period?
A higher discount rate reduces the present value of future cash flows, potentially increasing the discounted payback period. Conversely, a lower discount rate makes future cash flows more valuable, leading to a shorter discounted payback period.


